One of the easiest ways to earn passive income is simply to let your capital make money for you.

There are places that will pay you to use your money, so that they don’t have to use their own.

Banks, for example, give you interest on your Fixed Deposits or Certificate of Deposits (FDs or CDs).

If you deposit, say $10,000 of your money with them, you will earn interest of a few percent per year.

This rate depends on what the Central Bank’s monetary policy is for that year, and will vary from year to year.

But typically FD/CD rates vary from 0.5% – 3% a year.

This is the Annual Percentage Rate (APR).

For ease of calculations, let’s assume the APR on your capital is 10% a year.

So if you have deposited $10,000 with the the banks, at the end of 12 months your capital would have earned $1,000.

You will have a balance of $11,000 ($10,000 capital + $1,000 interest).

Now if you can COMPOUND your interest earned on your capital up to a certain time before the end of the year is up, by adding the interest to your capital to earn the same interest again, you will naturally earn more at the end of 12 months as you will be earning interest on a higher capital.

The total interest you will be earning if you compound your interest this way is called the Annual Percentage Yield (APY).

So if you can compound your interest earned every MONTH by adding it to your capital to earn interest again on the bigger capital, you will earn more than if you didn’t compound your interest.

If you can compound your interest every WEEK, you will earn more than if you did this every month.

If you can compound your interest every DAY, you will earn more than if you did this every week.

So the more often you compound your interest, the more money you will earn on your capital at the end of one year.

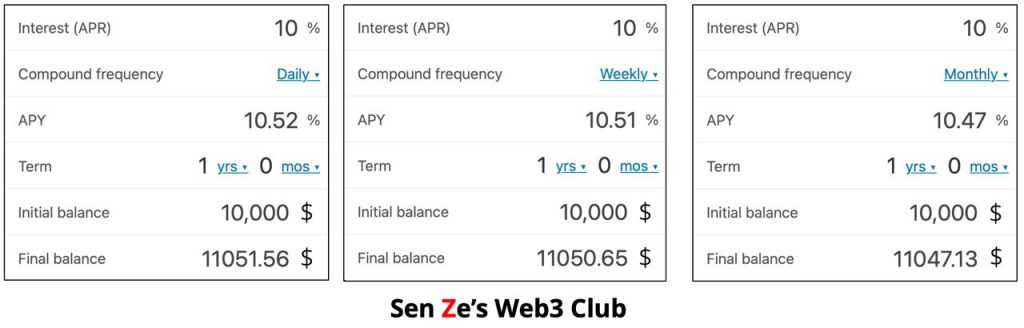
So instead of only getting $11,000 at the end of one year without compounding your interest, if you compound your yearly interest on:

1. A monthly basis

• • You will earn a total of $1,047.13 in interest at the end of 12 months.

• • You will have a balance of $11,047.13 at the end of 12 months.

• • Your APY is 10.47%.

2. A weekly basis

• • You will earn a total of $1,050.65 in interest.

• • You will have a balance of $11,050.65.

• • Your APY is 10.51%.

3. A daily basis

• • You will earn a total of $1,051.56 in interest.

• • You will have a balance of $11,051.56.

• • Your APY is 10.52%.

See attached images comparing APR and APY, depending on when you compound your interest:

Now if your APR is double, at 20% a year, then your APY will naturally be much higher.

But note the APY will be not be a doubling of the previous APY for an APR of 10% a year — it will be a bit higher. See the chart below for comparison: